Introduction to machine learning


2021

Dr. Rene Staritzbichler

Machine learning

What is machine learning?


Optimization of mathematical model by usage of data

  • Aliases:
    • 'pattern recognition'
    • 'data mining', 'data evaluation'
  • Goals:
    • explain data
    • predict data

Tasks

  • discrete data: classification
  • continuous data: regression
  • complexity reduction
  • encryption

Main classes

Discrete data:


good bad
alive dead
having disease X not having disease X

Continuous data:

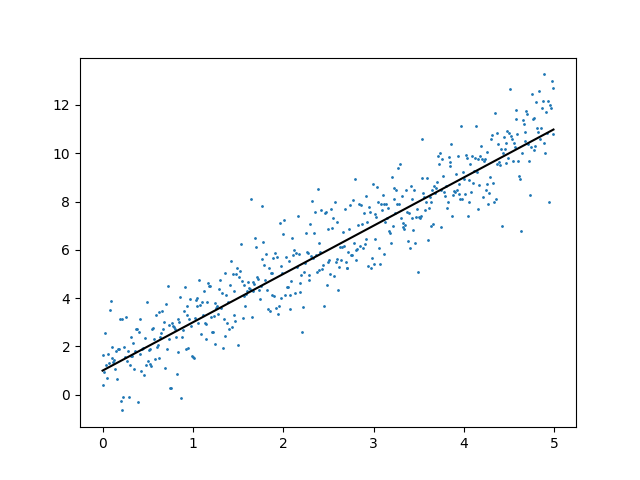
Basic mathematical principle

  • a basic mathematical function

    • $y = f(x)$

  • a deterministic relation or law of nature, e.g. F = ma
  • a more complex mathematical function

    • $y = f(x,c), \qquad \text{where c are free inner parameters} $

  • outcome depends on inner parameters
  • machine learning is the optimization of inner parameters

What is learning?

\[\begin{aligned} M(\boldsymbol{X}) & = y_{pred} \\ \epsilon & = \sum_{i=1}^{n} ( y_{pred, i} - y_{known, i} )^2 \\ \boldsymbol{X} & \in \mathbb{R}^{n \times m} \\ y_{pred/known} & \in \mathbb{R}^{n \times k} \end{aligned} \]

learning is the minimization of the error between known and calculated values.

Example

Definitions

  • X: input data matrix
    • columns: m features, e.g. age, weight, size, ...
    • rows: n samples, e.g. patients
  • ypred: calculated output
    • continuous: probability
    • discrete: class
  • yknown: available reference data
  • n: number of samples in reference data set
  • k: dimension of output

Types of learning algorithms

Supervised learning

  • expected outcome used as reference data X
  • training of model to minimize error

Unsupervised learning

  • no expected outcome X
  • instead quantification by e.g.
  • distance / similarity / variance

Unsupervised learning

  • Clustering
  • Hidden Markov Models
  • Principle Component Analysis

Supervised learning

  • Descision trees
  • (Logistic) Regression
  • Neural Networks
    • Convolutional NN
    • Graph NN
    • Recurrent NN
  • Support Vector Machines

Linear regression

  • fit a straight line through data

    \[ y = a \cdot x + b \]

  • minimize error
\[ \epsilon = \sum_{i=1}^{n} (y^{(i)} - \tilde{y}^{(i)} )^2 \]

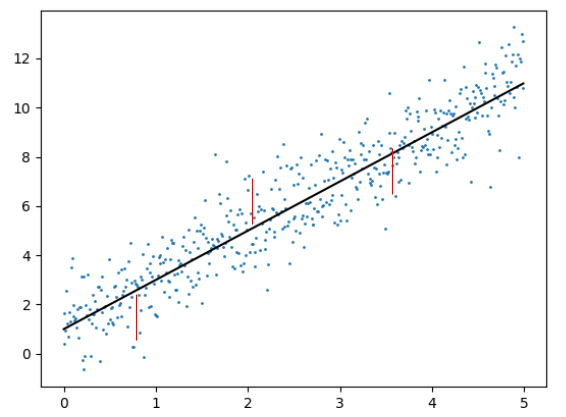
Cost function

choose function with simple derivatives

\[\begin{aligned} h(x) & = y = w_0 + w_1 x_1 + w_2 x_2 + \ldots \\ L & = \frac{1}{2n}\sum_{i=1}^{n} (h(x^{(i)}) - \tilde{y}^{(i)} )^2 \end{aligned} \]

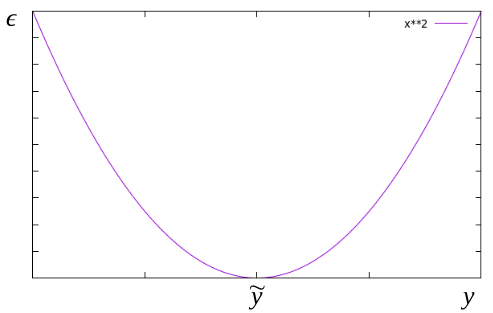
Steepest descent

follow the gradient :: backpropagation

\[\begin{aligned} w_j & = w_j - \alpha \frac{\partial L}{\partial w_j} \\ w_j & = w_j - \frac{\alpha}{n} \sum_{i=1}^{n} (h(x^{(i)} ) - \tilde{y}^{(i)} ) x_j^{(i)} \end{aligned} \]

Overcoming linearity

substitution of non-linear terms

allows to use linear math

\[\begin{aligned} y & = w_0 + w_1 x + w_2 x^2 + \ldots \\ x & = x_1,\quad x^2 = x_2, \quad \ldots \\ y & = w_0 + w_1 x_1 + w_2 x_2 + \ldots \\ \end{aligned} \]

Classification

  • separating groups of data points
  • $1^{st}$ order: line or plane
  • higher order: non-linear surfaces

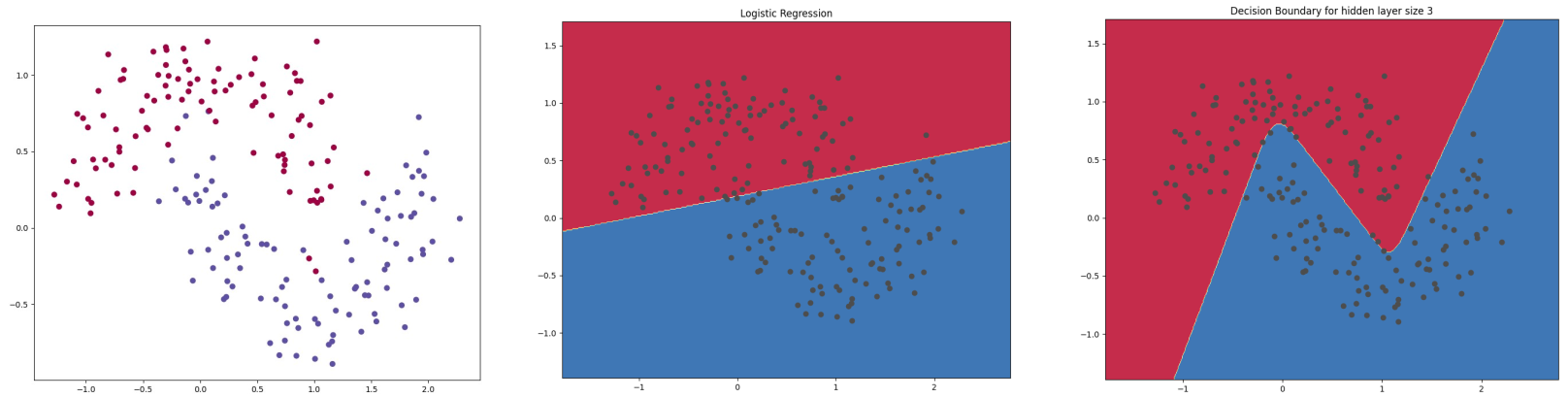
Logistic regression

apply sigmoid 'acitivation' function

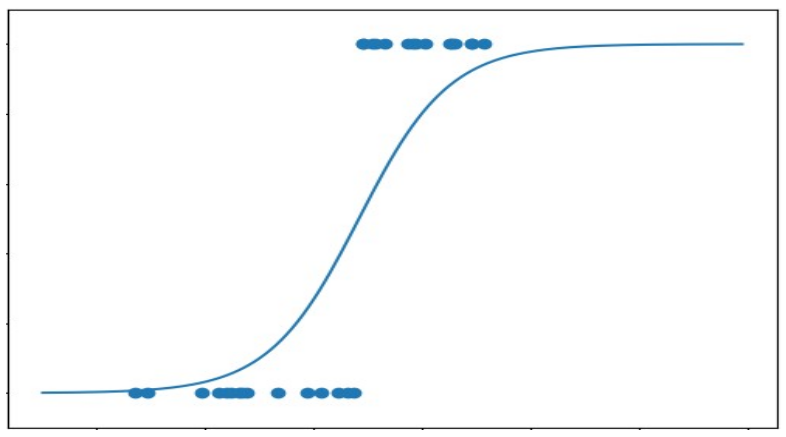
otherwise same approach as linear regression

Logistic regression

\[\begin{aligned} y & = w_0 + w_1 x + w_2 x_2 + \ldots \\ \sigma (z) & = \frac{1}{1+e^{-z}} \\ h(x) & = \sigma (w_0 + w_1 x + w_2 x_2 + \ldots ) \\ L & = \frac{1}{2n}\sum_{i=1}^{n} (h(x^{(i)}) - \tilde{y}^{(i)} )^2 \\ w_j & = w_j - \alpha \frac{\partial L}{\partial w_j} \end{aligned} \]

Artificial neural networks

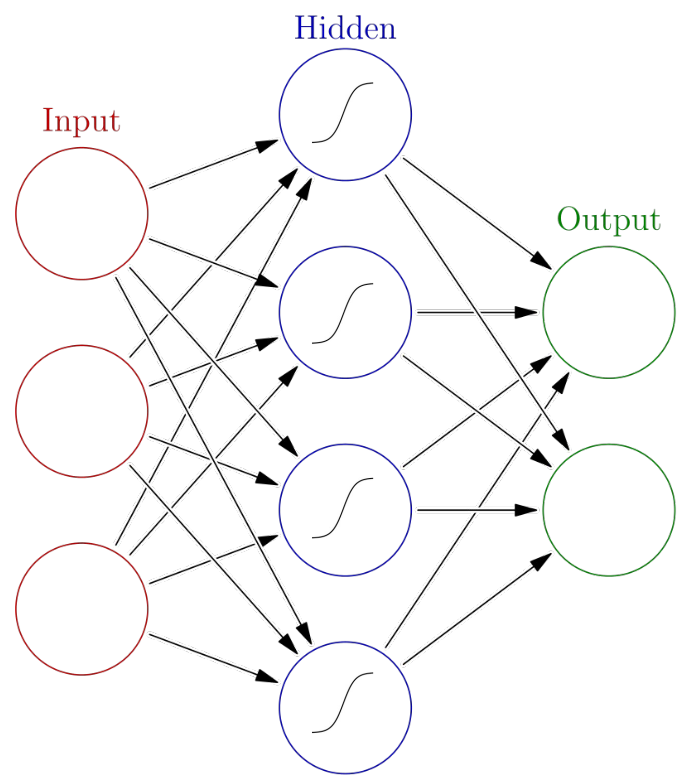
Forward propagation


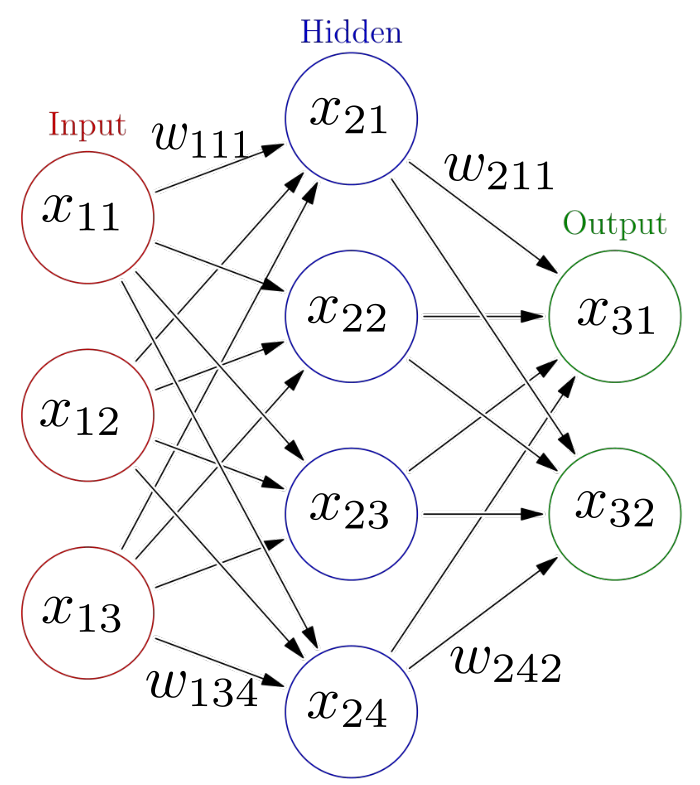
\[\begin{aligned} x_{21} & = \sigma ( w_{111}x_{11} + w_{121} x_{12} + w_{131} x_{13} )\\ x_{22} & = \sigma ( w_{112}x_{11} + w_{122} x_{12} + w_{132} x_{13} )\\ x_{23} & = \sigma ( w_{113}x_{11} + w_{123} x_{12} + w_{133} x_{13} )\\ x_{24} & = \sigma ( w_{114}x_{11} + w_{124} x_{12} + w_{134} x_{13} )\\ \\ x_{31} & = \sigma ( w_{211}x_{21} + w_{221} x_{22} + w_{231} x_{23} + w_{241} x_{24}) \\ x_{32} & = \sigma ( w_{212}x_{21} + w_{222} x_{22} + w_{232} x_{23} + w_{242} x_{24}) \end{aligned}\]

Iterative learning

    Forward propagation

    • multi-dimensional logistic regression

    Backward propagation

    • multi-layer steepest descent

Practical considerations

  • train and test data
  • overfitting
  • data scaling
  • regularization

Train and testdata

Overfitting

Data scaling

Regularization

Analyzing results

  • sweet confusion (matrix)
  • receiver operator curve
  • significance

Confusion matrix

'Artifical Intelligence'

  • could computers become concious?
  • could they feel and think the way we do?

Alan Turing 1912-54

  • pioneer of computer technology
  • major impact on $2^{nd}$ worldwar
  • Turing test ('imitation game'): when a human cannot distinguish whether he speaks to a human or a machine, the machine has passed the test

Why you don't qualify as judge

  • we notoriously project our hopes and fears onto everything
  • we love to identify with movie characters, project our emotions onto pets, fantasy creatures, smileys...
  • we are highly biased to 'yes, they can'

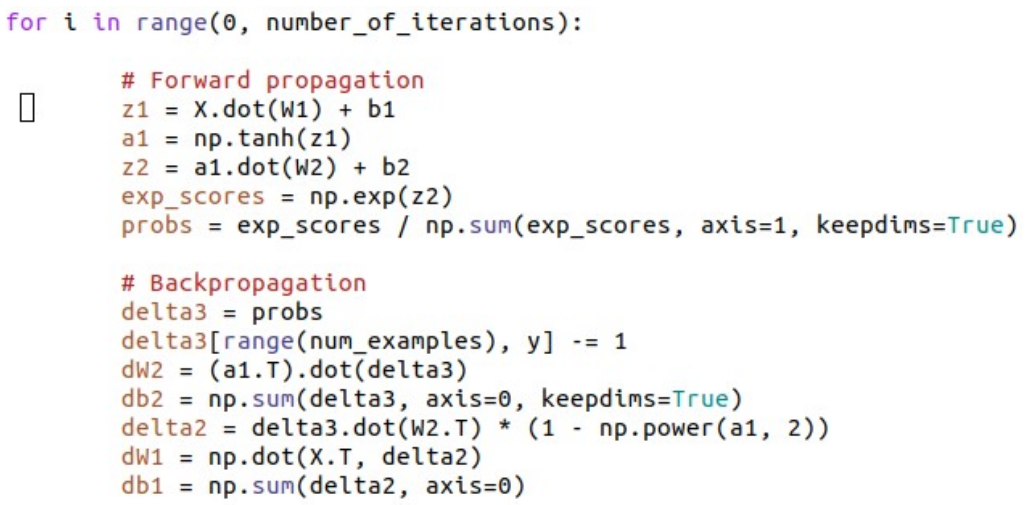
The god code?

can this snippet create a sentient being?

Considerations

  • could an imitation itself become what it imitates?
  • switching on/off
  • $\infty$ replicas, 100% identical

Cheers!